EM
Aryabhatta Knowledge University (AKU)Mechanical EngineeringEngineering MechanicsSolved Exam Paper 2019 Question. How would you find out the linear velocity of a rotating body?The linear speed of a point on a rotating object depends on its distance from the center of rotation. The angular speed is the angle that an object moves through in a certain amount of time. The angular speed has units of radians per second (rad/s). There are 2π radians in a full circle. At a distance r from the center of the rotation, a point on the object has a linear speed equal to the angular speed multiplied by the distance r. The units of linear speed are meters per second, m/s.Linear speed = angular speed x radius of the rotationv = ωrv = linear speed (m/s)ω = angular speed (radians/s)r = radius of the rotation (m)Question. Describe the phenomenon of combined motion of rotation and translation with a suitable exampleRolling Motion: • A motion that is a combination of rotational and translational motion, e.g. a wheel rolling down the road. • Will only consider rolling with out slipping.
For a disk or sphere rolling along a horizontal surface, the motion can be considered in two ways: I. Combination of rotational and translational motion: • Center of mass moves in a translational motion. • The rest of the body is rotating around the center of mass.II. Pure Rotational Motion: • The whole object is revolving around a point on the object in contact with the surface. • The point of contact changes with time.
When the object makes one complete revolution, the object has moved a distance equal to the circumference, and each point on the exterior has touched the ground once. • When the object rotates through an angle q, the distance that the center of mass has moved is: s = R𝛳 vcm = R d𝛳 dt = Rw where w is the angular velocity of one object rotating about its center of mass. This looks very similar to the relationship between angular velocity and the translational velocity of a point on a rotating object:v = Rw • vcm is the velocity of the center of mass with respect to the ground for the rolling motion. • v is the velocity of a point on the object with respect to the axis of rotation. The velocity of any point on the disk as seen by an observer on the ground is the vector sum of the velocity with respect to the center of mass and the velocity of the center of mass with respect to the ground: v gnd = v rel cm + v cm (1)
Question. State the laws of motion. Discuss the first law in the light of second lawThe first law of motion implies that things cannot start, stop, or change direction all by themselves. It requires some force from the outside to cause such a change. This property of massive bodies to resist changes in their state of motion is called inertia. Newton’s first law is also known as the law of inertia.Newton’s 1st law states that a body at rest or uniform motion will continue to be at rest or uniform motion until and unless a net external force acts on it.The second law of motion describes what happens to the massive body when acted upon by an external force. The 2nd law of motion states that the force acting on the body is equal to the product of its mass and acceleration.Newton’s 2nd law states that the acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.Newton’s second law describes precisely how much an object will accelerate for a given net force.Mathematically, we express the second law of motion as follows:f ∝ dP/dt⇒f ∝ (mv−mu)/t⇒f ∝ m(v−u)t⇒f ∝ ma⇒f = kmaIn the equation, k is the constant of proportionality, and it is equal to 1 when the values are taken in SI unit. Hence, the final expression will be,F = maThe third law of motion describes what happens to the body when it exerts a force on another body.The Newton’s 3rd law states that for every action there is an equal and opposite reaction.When two bodies interact, they apply force on each other that are equal in magnitude and opposite in direction. To understand Newton’s third law with the help of an example, let us consider a book resting on a table. The book applies a downward force equal to its weight on the table. According to the third law of motion, the table applies an equal and opposite force on the book. This force occurs because the book slightly deforms the table; as a result, the table pushes back on the book like a coiled spring. Newton’s third law of motion implies the conservation of momentum.Question. Define mass moment of inertia and kinetic energy of rotationMass moment of inertia also known as rotational inertia is a quantity that is used in measuring a body’s resistance to a change in its rotation direction or the angular momentum. It basically characterizes the acceleration undergone by an object or solid when torque is applied. The mass moment of inertia is usually denoted by the letter I.
II) Oblique impact: When two bodies, moving along different lines, collide the impact is called oblique impact.
III) Line of impact: The instant when two bodies just collide, the line joining their centres is called the line of impact.
Question. Prove the parallel axis theorem in determination of moment of inertia of areas with the help of neat sketchParallel axis theorem states thatThe moment of inertia of a body about an axis parallel to the body passing through its center is equal to the sum of moment of inertia of body about the axis passing through the center and product of mass of the body times the square of distance between the two axes.Parallel Axis Theorem FormulaParallel axis theorem statement can be expressed as follows:I = Ic + Mh2Where,I is the moment of inertia of the bodyIc is the moment of inertia about the centerM is the mass of the bodyh2 is the square of the distance between the two axesLet Ic be the moment of inertia of an axis which is passing through the center of mass (AB from the figure) and I be the moment of inertia about the axis A’B’ at a distance of h.Consider a particle of mass m at a distance r from the center of gravity of the body.Then,Distance from A’B’ = r + hI = ∑m (r + h)2I = ∑m (r2 + h2 + 2rh)I = ∑mr2 + ∑mh2 + ∑2rhI = Ic + h2∑m + 2h∑mrI = Ic + Mh2 + 0I = Ic + Mh2Hence, the above is the formula of parallel axis theorem.Parallel Axis Theorem of RodThe parallel axis theorem of rod can be determined by finding the moment of inertia of rod.Moment of inertia of rod is given as:I = 13 ML2The distance between the end of the rod and its center is given as:h = L2Therefore, the parallel axis theorem of rod is:Ic = 13ML2 – ML22Ic = 13ML2 – 14ML2Ic = 112 ML2Question. How will you distinguish between static friction and dynamic friction?
Question. What do you understand by the term “energy”? Explain various form of mechanical energiesBasically, energy is the ability to do work. While it could not be created nor destroyed, energy could be transferred or change. By being transferred to an object, it is able to do work on such object. In order to stay alive, living things such as humans require available. for humans, various forms of energy are needed from food to energy resources such as fossil fuels. Humans, and other organisms, also need energy in order to move and change in position. This where mechanical energy comes in.Mechanical energy is a form of energy possessed by an object due to its position or motion. Objects have mechanical energy whether they move or stay in position relative to a zero potential energy position. This means that any object that possesses mechanical energy – whether through movement or due to its position – could do work. Work is described here as the movement of an object when a force is applied to it.The mechanical energy of an isolated system – whether a physical system or a thermodynamic system – remains constant in time as long as the system is devoid of non-conservative forces such as friction. Though mechanical energy could not be created nor destroyed in an isolated system, it could be converted into other forms of energy.The form of mechanical energy that is possessed by objects which are in motion is called kinetic energy. An object that is in motion – whether it is horizontal or vertical motion – possesses kinetic energy. Its name was derived from the Greek word “kinesis” which means “motion.”Kinetic energy may come in various forms. The first form is rotational kinetic energy, the energy that is produced due to rotational motion. The second form is vibrational kinetic energy which is generated due to the movement of vibrations. The third is translational kinetic energy, the energy produced due to the motion from one location to another.The type of mechanical energy that is possessed by objects at rest, or due to their position, is called potential energy. It could also be the stored energy which an object has. It was introduced by William Rankine, a 19th-century engineer, and physicist.Potential energy comes in three forms – gravitational potential energy, electric potential energy, and elastic potential energy.Gravitational potential energy refers to the energy that is stored in objects due to their vertical position. Such energy is stored due to the gravitational pull of the Earth for the objects.Electric potential energy could be attained when different or alike charges repel or attract each other. The charges could either be positive or negative. Opposite charges attract each other while similar charges repel each other.Elastic potential energy, on the other hand, refers to the energy that is stored in elastic materials due to stretching and compression. The amount of stored elastic potential energy could be correlated to the amount of stretch of the device.Both kinetic and potential energy are essential components of the universe. They affect the movement and position of particles within the space-time fabric. Kinetic energy, in particular, is significant because it affects the movement of matter, down to the atomic level. On the other hand, potential energy could help determine the form of existence of matter at the atomic level.Question. What is simple pendulum? Under what conditions its motion is regarded as simple harmonic? A point mass attached to a light inextensible string and suspended from fixed support is called a simple pendulum. The vertical line passing through the fixed support is the mean position of a simple pendulum.The vertical distance between the point of suspension and the centre of mass of the suspended body (when it is in mean position) is called the length of the simple pendulum denoted by L.A simple pendulum is a mechanical arrangement that demonstrates periodic motion. The simple pendulum consists of a small bob of mass ‘m’ suspended by a thin string secured to a platform at its upper end of length L.
|
|
|
● Mass Moment of Inertia depends on the body’s mass and the location of the mass.
● If the distance of the mass is farther from the rotational axis, the mass moment of inertia will be relatively larger.
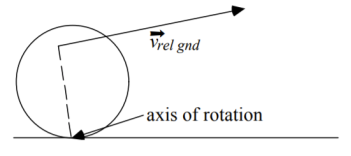
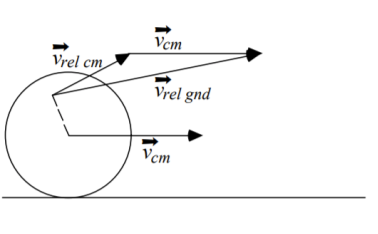
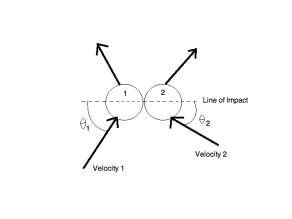
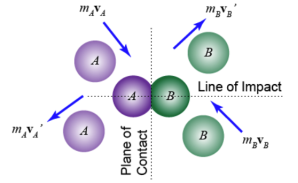
The kinetic energy of a rotating body can be compared to the linear kinetic energy and described in terms of the angular velocity. The extended object’s complete kinetic energy is described as the sum of the translational kinetic energy of the centre of mass and rotational kinetic energy of the centre of mass. The rotational kinetic energy is represented in the following manner for a constant axis of rotation.Rotational energy occurs due to the object’s rotation and is a part of its total kinetic energy. If the rotational energy is considered separately across an object’s axis of rotation, the moment of inertia is observed. Rotational energy also known as angular kinetic energy is defined as:The kinetic energy due to the rotation of an object is part of its total kinetic energy. Rotational kinetic energy is directly proportional to the rotational inertia and the square of the magnitude of the angular velocity. A rolling object has both translational and rotational kinetic energy.Question. What are the various types of impacts? Discuss any one of themI) Direct impact: When two bodies, moving along the same line, collide the impact is called direct impact.
|
|
|
Basis for Comparison | Static Friction | Kinetic Friction |
Basic | It is associated with body at rest. | It is associated with motion of object. |
Magnitude | More | Comparatively less |
Denoted as | Fs | Fk |
Expression | μsFN | μkFN |
Magnitude of force | Dependent | Independent |
Nature | It is opposition to the beginning of motion. | It is the opposition relative to motion of the body. |
Value | Can be zero. | Can never be zero. |
Behaviour | Shows linear increase up to a maximum value. | Shows invariable nature and remains constant. |
When it acts | In the absence of relative motion. | In the presence of relative motion. |
Example | Pen placed on the table. | Moving a pen over a table top. |
● The oscillatory motion of a simple pendulum: Oscillatory motion is defined as the to and fro motion of the pendulum in a periodic fashion and the centre point of oscillation known as equilibrium position.
● The time period of a simple pendulum: It is defined as the time taken by the pendulum to finish one full oscillation and is denoted by “T”.
● The amplitude of simple pendulum: It is defined as the distance travelled by the pendulum from the equilibrium position to one side.
● Length of a simple pendulum: It is defined as the distance between the point of suspension to the centre of the bob and is denoted by “l”.
Many physical systems exhibit simple harmonic motion (assuming no energy loss): an oscillating pendulum, the electrons in a wire carrying alternating current, the vibrating particles of the medium in a sound wave, and other assemblages involving relatively small oscillations about a position of stable equilibrium. The motion is called harmonic because musical instruments make such vibrations that in turn cause corresponding sound waves in air. Musical sounds are actually a combination of many simple harmonic waves corresponding to the many ways in which the vibrating parts of a musical instrument oscillate in sets of superimposed simple harmonic motions, the frequencies of which are multiples of a lowest fundamental frequency. A specific example of a simple harmonic oscillator is the vibration of a mass attached to a vertical spring, the other end of which is fixed in a ceiling. At the maximum displacement −x, the spring is under its greatest tension, which forces the mass upward. At the maximum displacement +x, the spring reaches its greatest compression, which forces the mass back downward again. At either position of maximum displacement, the force is greatest and is directed toward the equilibrium position, the velocity (v) of the mass is zero, its acceleration is at a maximum, and the mass changes direction. At the equilibrium position, the velocity is at its maximum and the acceleration (a) has fallen to zero. Simple harmonic motion is characterized by this changing acceleration that always is directed toward the equilibrium position and is proportional to the displacement from the equilibrium position. Furthermore, the interval of time for each complete vibration is constant and does not depend on the size of the maximum displacement. In some form, therefore, simple harmonic motion is at the heart of timekeeping.To express how the displacement of the mass changes with time, one can use Newton’s second law, F = ma, and set ma = −kx. The acceleration a is the second derivative of x with respect to time t, and one can solve the resulting differential equation with x = A cos ωt, where A is the maximum displacement and ω is the angular frequency in radians per second. The time it takes the mass to move from A to −A and back again is the time it takes for ωt to advance by 2π. Therefore, the period T it takes for the mass to move from A to −A and back again is ωT = 2π, or T = 2π/ω. The frequency of the vibration in cycles per second is 1/T or ω/2π. Question. Define the following terms:The applied torque needed to produce a unit angle of twist in a circular elastic material; a measure of a body's resistance to torsion.Rigidity is the maximum resistance an object can offer before it deforms, in other words, it is the minimum force required to deform an object.
Torsional Rigidity : The minimum force required to deform an object by twisting through a unit dimension..(in this case, for twisting the dimension is in angle of twist)
Polar moment of inertiaPolar Moment of Inertia is a measure of an object’s capacity to oppose or resist torsion when some amount of torque is applied to it on a specified axis. Torsion, on the other hand, is nothing but the twisting of an object due to an applied torque. Polar moment of inertia basically describes the cylindrical object’s (including its segments) resistance to torsional deformation when torque is applied in a plane that is parallel to the cross-section area or in a plane that is perpendicular to the object’s central axis.
If we put it in simple terms polar moment of inertia is the resistance offered by a beam or shaft when it is being distorted by torsion. This opposition usually arises from the cross-sectional area and it should be noted that it does not depend on the material composition. If the polar moment of inertia is of higher magnitude then the torsional resistance of the object will also be greater. More torque will be required to turn the shaft at an angle.
0 matching results found