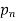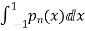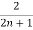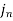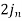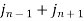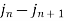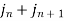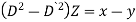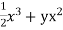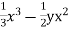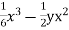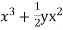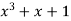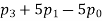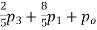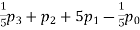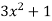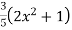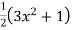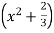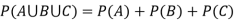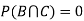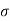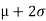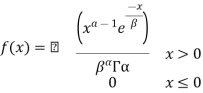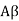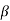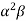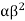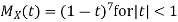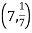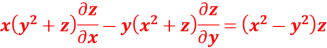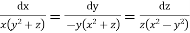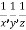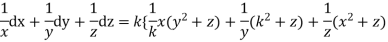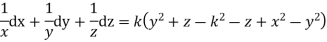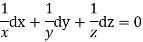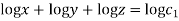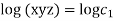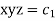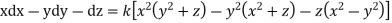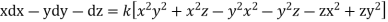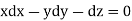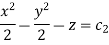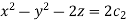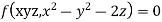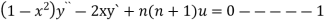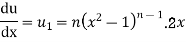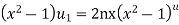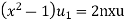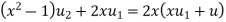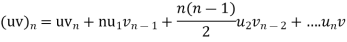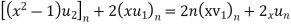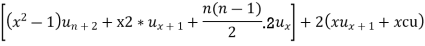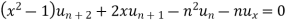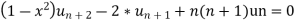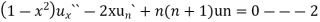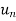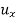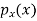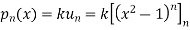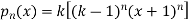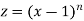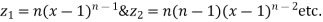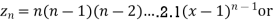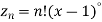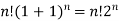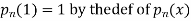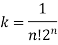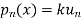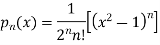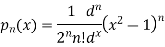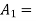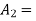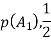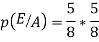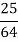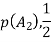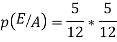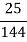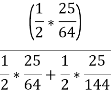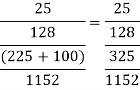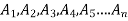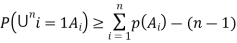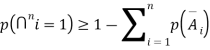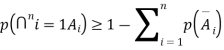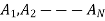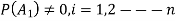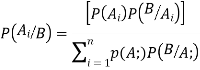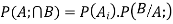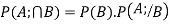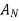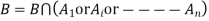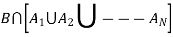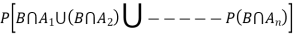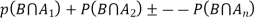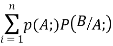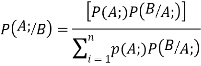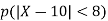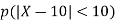1. Q1. Choose the correct answer (any seven):

1. If is the legendre polynomial of first kind, then the value of is.

1. 0
2. 
3. 2
4. 1

b.     If is the bessel’s function of first kind, then the value of , is

c.      The particular integral of , is

d.     The function in terms of legendre polynominal is equal to

e.     Let the joint probability density functions of the continuous random variable X and Y be.

Then the margin density of X is.

f.        If

g.     Let A,B and C be any three mutually exclusive events. Which one of the following is incorrect?

h.     If is the mean and is the standard deviation of a set of measurement which are normally distributed , then percentage of measurement within the range

1. 98
2. 95.44
3. 99.73
4. 95

i.        If the density function of gamma distribution is

Then variation is equal to.

j.        The moment generating function of a continuous random variable X be given as

Then its mean and variance is

Q2. A) Solve     

Answer:

Choose the multipliers as

On integration

now again choose the multipliers as x,y,-1

on integration

Now on combining both eq. we get a general solution

2.    Q3. State and prove Rodrigues formula .

Sol- we derive a formula for the legendre polynomials

Formula

Now proof

Let

We shall first establish that the nth derivation of u, that is is a sol of the legendre differentiate eq.

Differ w.r. to x

Or

i.e

Diff. w.r. to x again, we have

Now differ. The result in timer by applying lebuitz theorem for nth derivation of a product given by

Or

This can be put in the form

Comparing 2 with 1 we conclude that is a solution of the legendre’s eq. it may be observed that U is a polynomial of degrees 2x & hence will be a polynomial  of degree x.

also which satisfies the legendre differentiate eq. is also a polynomial of degree x.

Applying Leibnitz theorem for the RHS we have

It should be observed that if

Putting x =1 in eq. 1 all the terms in RHS become zero except the last term which becomes

Q4. A coin is tossed. If it turns up H, two balls will be drawn from urn A otherwise 2 balls will be drawn from urn B. urn A contains 3 red and 5 blue balls , urn B contains 7 red and 5 blue balls. What is the probability that urn A is used , given that both balls and blue? (find in both cases, when balls were chosen with replacement and without replacement).   

   Sol- let us define the following events

urn A is chosen

urn B is chosen

E= two blue balls are drawn (with reputation)

Then we have

So,

 (b) for event

Prove that

Q5. State and prove bayes theorem.

 Sol. –it states that “If are n mutually exclusive event with & B is any other event which can occurred with A or or then we have,

Proof- by compound theorem of probability ,

We get

Or

Given that , B is any other event which occur with A or A; or ….. i.e

Again from II

                                          7

(b) a random variable X follows binominal distribution with parameter n=40 and use chebyshev’s inequality to find bounds for.

a.

b.